2003年夏天，我由紐西蘭的奧克蘭機場要搭機返國，因時間尚早，所以在機場的商店街閒逛，無意間在玩具部門發現有個塑膠袋裡裝了一個瓶蓋和兩根透明塑膠管（圖1）。塑膠袋上附了一張硬紙板，簡單畫了一張圖，說明只要自備兩個保特瓶，就可以製作出一個雙面噴泉。我很感興趣，當場買下，然後才去搭機。

圖1 一個瓶蓋和兩根透明塑膠管

回國後，找了兩個空的保特瓶，就在自家浴室試驗起來，由於商人所附的圖並未說明清楚，所以試了幾次才成功。

後來，我在國立新莊高中的科學營演示這個實驗，學生很感興趣。說真的，這個實驗還蠻有趣的，水往低處流並不稀奇，但噴泉的水是向上流的，為什麼水會向上流呢？如果你想懂了，才有可能成功裝置出噴泉，否則就算整套設備都交到你手裡，還是無法成功演示雙面噴泉。所以，我常常在表演完後，把整套裝置拆解掉，然後徵求一名志願的學生上台來操作，看看他是否能成功地使演示雙面噴泉。多年來，僅有兩名學生第一次就成功演出，一名是國立武陵高中的學生，一名是台北縣私立東山高中的學生。有趣的是，我請武陵高中那位同學解釋雙面噴泉的原理時，他聳聳肩表示：「我也不知道，隨便裝一裝就成功了。」我當場就請他幫我買樂透。

我買到的器材中，瓶蓋沒什麼特別，它裡面有兩個孔（圖2），可以分別插入兩根塑膠管，而且這個瓶蓋兩面都有螺紋，可以在兩個方向各旋上一個空保特瓶。

圖 2 瓶蓋有兩個孔，雙面都有螺紋

那兩根塑膠管其實暗藏玄機，管子長度26.5公分，在其中一端2公分及2.5公分的地方，各有一環針孔，每環有4個針孔，總共8個針孔（圖3）。

圖 3 塑膠管上有小孔

如果拿到器材的人沒有仔細觀察，就不容易發現這幾個針孔，胡亂組裝的結果，失敗率很高。

表演時，在其中一個保特瓶裝茶水至八分滿，使用茶水的原因，是為了把水染色，便於觀察。瓶蓋的兩個孔分別插入兩根塑膠管，恰好插入即可，不要伸出太多（圖4）。

圖4瓶蓋的兩個小孔分別插入兩根塑膠管

要注意，兩根塑膠管有針孔的一端要接近瓶蓋（圖5），這是整個實驗成敗的關鍵。

圖5有針孔的一端要接近瓶蓋（圖中黑色框框處即為針孔）

接下來，把另一個空保特瓶旋在瓶蓋的另一端，裝置就完成了（圖6）。

圖6 另一個空保特瓶旋在瓶蓋的另一端，裝置就完成了

表演時，只要翻轉上下兩個保特瓶的相對位置，上瓶就會出現噴泉（圖7）。

圖7 翻轉上下兩個保特瓶的相對位置，上瓶就會出現噴泉

雙面噴泉的原理為：當我們翻轉保特瓶時，上瓶的茶水經其中一根塑膠管向下流，下瓶的氣體因受水擠壓，根據波以耳定律，氣體體積減少，壓力會變大。受擠壓的空氣經由另一根塑膠管向上流，氣流經過針孔時，正好帶動經由針孔滲入的水，順勢把水向上帶到管口附近噴出，就形成噴泉。等所有的水都流入下瓶後，只要再次翻轉上下兩個保特瓶的相對位置，就會再次出現噴泉，所以我把它命名為「雙面噴泉」。

很多學生看完這個有趣的實驗後，會很想自己擁有一個雙面噴泉，其實自己動手製作一個雙面噴泉也不難。先到花店去「要」兩根氣球棒（其實我每次都跟老闆說我要用買的，但是因為只要兩根，老闆也不知道該怎麼算錢，就送給我了）。然後視瓶子大小剪成合宜的長度，如果你是使用2升的家庭號空保特瓶，那麼長度就用26.5公分；若用小瓶子，長度就剪短一些。然後用火加熱鐵製迴紋針，用熱的迴紋針刺入氣球棒的一端，就會出現針孔（圖8），可多刺幾個，針孔數目不影響實驗成敗，但針孔多，噴泉會比較壯觀。兩段氣球棒同樣方法，在其中一端各刺上數個針孔。

圖8 熱的迴紋針刺入氣球棒就會出現針孔（圖中方框即為針孔）

找來兩個空保特瓶，先把其中一個塑膠瓶蓋用熱的迴紋針刺出兩個小孔，再用剪刀的尖刃把小孔擴大到能插入氣球棒即可（圖9）。

圖9 在塑膠瓶蓋上挖出兩個孔

把兩個瓶蓋反面並排，依第一個瓶蓋小孔的位置畫出第二個瓶蓋上小孔的位置，這樣就可以確保兩個瓶蓋的小孔能夠密合了。再依上述方法在第二個瓶蓋上挖出兩個小孔。把氣球棒插入小孔，同樣要注意，有針孔那一端要靠近瓶蓋，但位於瓶內，試驗後如果會漏水，要用熱熔膠補好。至此，自製雙面噴泉的道具就完成了，玩法則與前述買來的雙面噴泉一模一樣（圖10）。

圖10 　自製雙面噴泉

「百變方塊」問世後約5年，坊間又出現另一種正方體造型的立體創意文宣，其零件改為8個大小相同的三角柱，但結構則是巧妙地仿製「百變方塊」的8個特定相接位置，此一造型上的改良，使得該設計不僅可如同「百變方塊」般不斷地翻轉循環，且可變化的造型更加多元（圖一）。由於零件的上下底為兩個全等的等腰直角三角形，而在翻轉的過程中，亦可見一大型的等腰直角三角形，故筆者將之命名為「百變三明治」。本文即介紹筆者將「百變三明治」串接於數學營的課程設計與教學心得分享。

（圖一）由「百變三明治」立體創意文宣翻轉而成的各種立體造型。

【教學目的】增進立體概念及空間思維；培養動手操作與合作學習的習慣。

【教學內容】a. 探究「一題多解」的正方形「火柴棒」創意思考遊戲。

　　　　　　  b. 認識並學習棋盤內方形數量問題的「降階」策略。

　　　　　　  c. 藝數Fun手玩---〈百變三明治〉DIY親體驗。

　　　　　　  d. 〈百變三明治〉vs.〈百變方塊〉。

【教學對象】國小高年級以上，分組上課，每組6-8人並給予編號。

【單元時間】90分鐘。

【操作教材】每組一盒火柴（或一包吸管）、每位學員一張〈百變三明治〉DIY。

【教學流程】

0. 課前準備：製作教學ppt.檔及數個大型的「百變三明治」模型。

1. 問題導引：引領學員回顧正方形的定義：平面上，同時滿足等邊和等角兩個條件的四邊形。提出問題搶答：請利用12根火柴棒（或等長的吸管）拼組正方形，但拼好的造型要剛好能組成一個中文字的結構。（火柴棒或吸管不可彎、不可折）

正解：有「口、品、田、回」等4字。

建議：答對的小組加分，以下皆同。經驗裡，「品」和「田」很快就出爐，「回」比較慢出現，至於「口」，則是時快時慢，但有時卻會意外地根本沒有人想到，算是一個有趣的教育現象。「火柴棒」原是此一類型題目傳統的「表達方式」，但因火柴已與絕大多數人的生活脫鉤，現在e世代的學員有些甚至從未看過、摸過，故教師可特別當教具收集，或改以吸管替代。原則上，各組備著一盒火柴或一包吸管即可，因為並非每位學員都需要依賴具體的操作才有答案。另在強調不可彎、折的限制條件時，教師不妨順帶說明數學上的「等長的線段」。

2. 分類＋問題導引：如下表，先引領學員分別將上題答案所含括的正方形數量作分類，然後提出問題討論：利用12根火柴棒（或等長的吸管）拼組正方形，請問還有哪些類型的答案？

說明：本題只是將上題「要能組成一個中文字結構」的條件移除，算是更開放式的提問，目的是希望能導引出「正方體」與「5 × 5棋盤」的答案（圖二a、b）。但多數學員可能受限於上題的思維模式，以致一時無法反應過來，不知要忙什麼，故上表特地留一些空格位置，供教師再次導引與說明，必要時，教師可視情況給予提示，例如：有無三度空間的答案？從「品」字的3個正方形還可以有哪些創意的變化？

正解：

（1）創思型的答案有：構成「正方體」的6個正方形（圖二a）、「5 × 5棋盤」的55個正方形（圖二b）、兩個「田」字的10個正方形（2大8小，圖二c），而堪稱一絕的答案，則是構成「正八面體」的3個正方形（圖二d）。

（2）靈活型的答案有：從「回」字演變而來的3個正方形（1大1中1小，圖二e）；從「品」字演變而來的4個正方形（3大1小，圖二f）、5個正方形（3大2小或3大1中1小，圖二g）、7個正方形（3大4小，圖二h）、8個正方形（3大2中3小…，圖二i）；從兩個「田」字演變而來的11個正方形（2大8中1小，圖二j）、9個正方形（2大7小，圖二k）、21個正方形（2大10中9小，圖二l）、17個正方形（2大10中4小1微，圖二l）…，其中，在兩個「田」字的演變思維下，通常會引發出「5 × 5棋盤」的靈感。

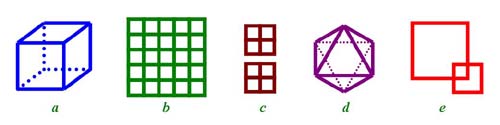
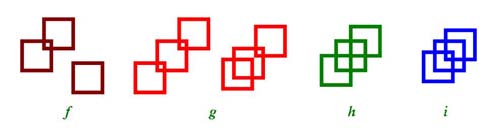
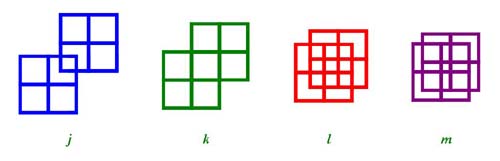
（圖二）利用12根吸管拼組正方形的「一題多解」。

建議：此題答案的種類眾多，創思型的答案較無脈絡可循，但靈活型的答案會形成一通百通的局面。由於一開始大家多未進入狀況，不易文思泉湧，故建議先讓各組學員內部互相討論，將答案彙整在講義上，然後分成幾回合，由指定號碼的學員上台呈現答案，同一回合的答案不分先後，只要不是之前已公布的皆可得分，藉此激勵各組追求卓越的意志，通常不超過兩回合，學員的思維便可從陸續公開的答案中活絡起來。（以上運作約20分鐘）

3. 深入探討：當上題的答案差不多山窮水盡之後，教師再分兩階段，以數回合的運作，由各組重新指定編號的學員上台自選並寫出某個答案所含正方形的數量（第一階段）及幾大幾中幾小的類型（第二階段），如此下來，壓軸的題目幾乎就剩「5 × 5棋盤」的分析探討。

說明：關於「5 × 5棋盤」內正方形的數量，或許在上題就有部分學員察覺出規律與特徵，但多數學員其實仍無法判斷對錯，如果教師只是公告答案就一筆帶過，那就太浪費這一題所要傳達的數學思維了。為了讓其他學員也能體認本題的數學境界，教師宜直接做教學導引，引領學員透過「降階」技巧，認識數學的規律之美。

建議：

（1）數數看：多數學員一開始為了搶時間，幾乎都採用此一策略，但很快就自動放棄了，因為盲目的數數，數多數少也沒判斷依據，即使數到最後，可能連自己也不敢確定答案的正確性。不過，偶有少數頭腦清晰且有耐性的學員，知道要分成邊長是1單位、2單位、3單位…的正方形來處理，然後用一點乘法概念，便可分析出5×5＋4×4＋3×3＋2×2＋1×1的規律。

（2）降階找靈感：在正式導引之前，教師可先拋出更誇張的問題：如果今天要算的不是5×5的棋盤，而是西洋棋的棋盤（8×8）或更複雜的圍棋的棋盤（18×18）？藉此傳達處理此一類型題目極為重要的「降階策略」。如圖三，教師透過互動，讓學員慢慢明瞭不論是18×18、8×8還是5×5的棋盤，其實都是同一類型的題目，因此，當初次面對「5×5棋盤」而不知所措時，不妨自動將難度降低一點，改為處理4×4棋盤的問題，萬一仍無頭緒，再繼續「降階」，改為3×3或2×2或1×1的棋盤，最後再逆向逐一分析其所含正方形的種類和數量，相信學員很快就會歸納出規律，並大膽猜測n×n棋盤有1×1＋2×2＋…＋n×n個正方形。

1×1棋盤有1個正方形，1＝1＝1×1；

2×2棋盤有5個正方形，5＝4＋1＝2×2＋1×1；

3×3棋盤有14個正方形，14＝9＋4＋1＝3×3＋2×2＋1×1；

4×4棋盤有30個正方形，30＝16＋9＋4＋1＝4×4＋3×3＋2×2＋1×1；

5×5棋盤有55個正方形，55＝25＋16＋9＋4＋1＝5×5＋4×4＋3×3＋2×2＋1×1；

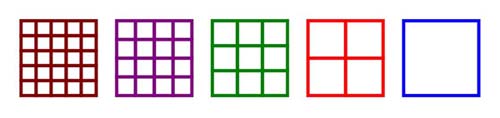
 （圖三）「5 × 5棋盤所含正方形數量」問題的漸進式思維。

4. 進階與推廣：當學員已抓到訣竅時，教師可再導引學員認識幾個相關的後續研究。

（1）n × n棋盤所含正方形數量的呈現方式：

 （2）n × n棋盤所含長方形的數量

 （3）n × n× n魔術方塊所含正方體的數量（圖四）。

 （4）n × n× n魔術方塊所含長方體的數量

（圖四）傳統正方體魔術方塊的各式切割：2 × 2、3 × 3、4 × 4、5 × 5。

建議：有關長方形或長方體數量的問題，因屬於現行高二數學「排列組合」的範圍，故筆者通常未加以著墨，僅是拋出問題並寫出結果，供有興趣的學員作回家功課。至於正方形或正方體數量的Σ公式，筆者多以「賣弄數學學問」的開玩笑方式介紹，目的只是希望策進學員精益求精的動力，所謂「學無止盡、學海無涯」，切勿自滿。而真正有花心思安排設計的，便是希望學員現學現賣，能把才抓到棋盤方形數量研究訣竅的「降階」策略，直接應用到魔術方塊所含正方體的數量研究上。（以上運作約20分鐘）

5. 〈百變三明治〉DIY：在前述動腦思考的活動告一段落之後，緊接著安排紙製DIY的操作。教師可從2×2魔術方塊的切割，引出「百變方塊」的神奇結構，然後再介紹改良版「百變三明治」的豐富造型，此時學員對於接下來的DIY操作早已躍躍欲試。教師除了說明剝、摺、黏、組等製作細節與透明膠帶的黏貼位置（圖五）之外，宜再提醒：黏貼透明膠帶時，各零件之間宜保留適當的均勻縫隙，且每個黏貼邊的正反兩面都應貼膠帶，方能牢固耐玩。

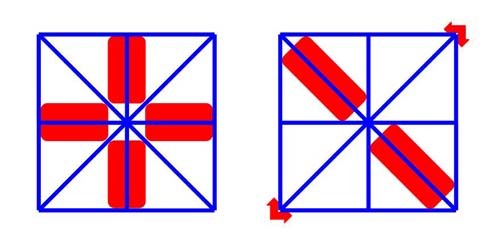
（圖五）「百變三明治」零件連接示意圖：正面4段膠帶（左）；底面＋側面各2段膠帶（右）。

當DIY陸續完成之後，教師可每組發數個「百變方塊」模型，供學員觀察比對，認識兩者結構上的異同，開啟改良發明的思維習慣。最後再透過加分方式，讓小組認識「百變三明治」各式可能的造型變化，並討論分析各形體間「等積求周」（註）的數學變化。

註：周長相同，求所圍面積大小變化的數學問題稱為「等周求積」，反之則為「面積相同，求周長大小變化的等積求周問題」，在此藉作「體積相同，求表面積大小變化」的推廣。

【相關閱讀】關於「百變方塊」的相關介紹，請參閱本刊第144期魔數專欄〈「百變方塊」趣味數學教學設計分享〉。

最近去美國開會，聽到一個非常有趣的臨床報告：一個病人在中風以後，她寫出來的字，字母、位置什麼都對，就是沒有母音，例如「男孩」這個字，她寫的是B_Y，知道空一格留給母音，但是寫不出母音來。因此，現在知道子音和母音儲存在大腦的不同位置。

這一類的病例，提供我們了解大腦對訊息的處理方式，尤其是記憶力的好壞，跟訊息在登錄時所下的功夫有關：記憶一般分成「登錄」、「儲存」、「提取」和「遺忘」四個階段，其中登錄最重要，受注意力和情緒影響。

美國是個講求實用的民族，所以腦科學進步到一個程度，對記憶有所了解後，就會有教育心理學家提出就記憶的本質去設計課程、改變教學。他們認為，要改善學習必須：

第一：先確定孩子的生理，是在最佳學習狀態。他們的口號是「要孩子學得好，要他睡得飽」，所以現在美國有十八個州把上課時間延後到九點才開始（各州不同），就是希望孩子一夜好眠，補充學習所需的神經傳導物質，如血清張素、正腎上腺素，使上課效果更好。

另外，因為睡眠跟情緒有直接關係，睡不夠的人會脾氣暴躁，所以青少年睡眠要特別充足，以免上課鬧事或打架。還有，睡眠週期會因荷爾蒙改變，青少年比較晚睡晚起，因此，學校調整作息時間，以配合學生身心發展。

第二：學生注意力不能維持很久，所以課堂上，十到十五分鐘講完一個核心主題後，就問學生問題，把剛講過的溫習一遍，確定學生聽懂了再繼續後面的課程。

研究發現，中間停頓問問題，可以把正要游離的記憶力抓回來，使接下來的十到十五分鐘專注聽講。我們老早就知道互動式教學有效，只是多少時間互動一次，倒是第一次看到實驗證據。當然，越小的孩子，注意力集中的時間越短，因此，需要中斷、重新凝聚注意力的次數得更多，難怪低年級的老師上課要又唱又跳。

第三：對有意義的東西，大腦才記得住；沒有意義的，只好死背。因此，老師要先知道學生的背景知識在哪個層次，從學生熟悉的生活層面切入，他們才會了解得快。所以，老師若能熟知所在社區的生活形態，舉例才能引起學生共鳴。

這一點，我頗有同感：很多去山地教書的老師，對當地居民的文化背景、生態知識了解不足，所以上起課來很辛苦，效果也不好。例如：山上沒有斑馬線，沒有紅綠燈，用它們來舉例就不恰當。

第四：一堂課不能教太多主題，而且一個主題要多舉幾個例子來加深孩子的印象。這些例子，最好由學生來提供，大家一起討論例子是否恰當；經過深層思考的記憶，存得最久。

在實驗上，我們已看到「溫故而知新」的神經機制：每九十分鐘如果能重複一次，記憶效果最好。又因為記憶是儲存在最初登錄的神經突觸上，所以登錄時所下的功夫越多，將來回憶的效果就越好。以前我父親常說，學習沒有捷徑，做學問要腳踏實地，一步一腳印，下的功夫越多，學問越紮實，真是很對。

從目前研究看來，沒有記憶不好這回事，只看登錄時下了多少功夫。父母不要老是罵孩子笨、記不住東西，只要把握上面所說的記憶生理機制，讓他多看、多聽，對訊息熟悉後，自然就登錄在孩子的腦子裡了。

◎本文轉載自國語日報97/08/26家庭版

性費洛蒙是昆蟲用來吸引異性的化學物質，農民利用昆蟲的性費洛蒙，發佈假消息，達到滅蟲的目的。利用這個概念，是否能趕走生活中所有令人討厭的昆蟲呢？ 文／楊嘉慧

近年來，無毒農業逐漸蔚為風潮，農民透過一種令昆蟲神魂顛倒的氣味引來害蟲，這氣味就是昆蟲的性費洛蒙。昆蟲會一路奔向氣味來源，農民便得以捕殺。這種迷惑昆蟲的性費洛蒙有什麼特性？它能誘殺害蟲，是否也能消滅蟑螂呢？

看不見的徵友啟事

性費洛蒙是腺體分泌的外激素，用以吸引異性。費洛蒙與我們熟知的激素不同，激素是影響生物體內各組織、細胞間作用的化學物質，費洛蒙則是同種個體間溝通的重要化學物質，如傳達警戒信號、食物地點、尋找伴侶等。中央研究院細胞與個體生物學研究所助研究員賀孝雍指出，昆蟲之間可以利用聲音（蟋蟀、蟬的鳴叫）、光訊號（螢火蟲）、行為姿態（如蜜蜂的8字舞）等進行溝通，但利用費洛蒙溝通消耗的能量少，可長時間分泌費洛蒙傳遞訊息，其氣味分子更可繞過障礙物做長距離傳送。

最早描述性費洛蒙現象的是19世紀的法國博物學家法布爾（Jean-Henri Fabre, 1823~1915）。有一天，法布爾發現將近40隻雄蛾竟在伸手不見五指的夜晚飛進實驗室，尋找一隻早上才羽化的雌蛾。為了查出雄蛾找到雌蛾的原因，他設計了幾個實驗。

法布爾將雌蛾放入不透氣的玻璃瓶，讓雄蛾看得見雌蛾卻聞不到氣味，結果沒有任何雄蛾被吸引過來；由此可知，雄蛾並非是透過視覺來尋找雌蛾。相較於雌蛾，雄蛾有很寬大的觸角，於是法布爾猜想牠們應該是透過觸角發現雌蛾，他將24隻雄蛾的觸角剪斷，讓牠們無法感受空氣中的氣味（雄蛾的嗅覺氣官在觸角上），果然雄蛾完全不被雌蛾吸引過來。法布爾還發現，雌蛾曾經待過的濾紙也會吸引雄蛾飛來。法布爾因此得出結論：吸引雄蛾的是雌蛾的氣味，而這個引誘異性的化學物質，後來被稱為性費洛蒙。

人工製造昆蟲香水

性費洛蒙是昆蟲羽化成蟲、達到性成熟且尚未交配時才會分泌，此時接收性費洛蒙的感應能力也較強。雌蟲和雄蟲都有可能釋放性費洛蒙，依昆蟲種類不同而各異。就鱗翅目昆蟲而言，一隻雌蛾只要分泌數奈克（10-9克）的性費洛蒙，便能讓數公里之遙的雄蛾感受到。

由於性費洛蒙具有聚集異性的特性，因此自然界早有某些動物模仿性費洛蒙的氣味，用以掠食昆蟲。例如流星錘蜘（Mastophora cornigera）就常模擬雌蛾散發的性費洛蒙氣味，吸引雄蛾自投羅網。又如農民利用性費洛蒙聚集害蟲，並加以捕殺，便能降低牠們的繁殖機率。

農民使用的性費洛蒙是以人工方式合成，因性費洛蒙具有「專一性」，不同種生物的性費洛蒙化學組成都不一樣，即使成份相同，組成比例也不一樣，才不會彼此干擾，因此要利用性費洛蒙捕殺害蟲，得先知道每一種害蟲的性費洛蒙化學結構與配方。

賀孝雍表示，破解性費洛蒙化學結構的程序相當繁複，方法也有很多種，其中一種是將羽化的成蟲放入玻璃瓶內，抽出成蟲所放出的氣味，附著在吸附劑上，再以溶劑將氣味成份溶解出來，接著進行分離與鑑定。由於性費洛蒙釋放的濃度也會影響集蟲的成效，因此在實驗室合成出性費洛蒙後，還需到田裡實驗，確定使用的濃度，才能有效吸引昆蟲。

現在農民常用的性費洛蒙除蟲法主要是「誘殺法」及「交配擾亂法」。誘殺法是將性費洛蒙放在內徑1毫米的塑膠管內，再放在黏蟲板上，或以紙盒、寶特瓶等製作陷阱，誘捕害蟲。交配擾亂法則是把高濃度的性費洛蒙放到田裡，迷惑雄蛾，讓雄蟲找不到雌蟲，無法交配、進而繁殖下一代；不過這種方法不像使用誘殺法可以馬上見到效果，需等到子代減少才知成果。

既然田裡的害蟲可以用性費洛蒙消滅，那麼是否也能以此法趕走家裡的蟑螂？賀孝雍表示，利用性費洛蒙控制害蟲是有條件限制的，它必須等害蟲長大才能進行消滅；而對於可進行孤雌生殖（不需交配即可產生後代）的害蟲，例如蚜蟲，就毫無用武之地；此外，由於此法只能在昆蟲的繁殖期間施用，生命週期長或已經交配過了的害蟲，性費洛蒙對牠們也不會有太大的吸引力。蟑螂的生命週期約一至二年，因此很難以此法消滅。

性費洛蒙雖然有上述缺點，但它是天然殺蟲劑，不會對環境造成污染與產生抗藥性，且具專一性，不會誤殺益蟲，因此仍值得被推廣與應用在農業上。

延伸閱讀

..........................................................................................................

《法布爾昆蟲記‧裝死》，楊世平審訂，遠流

《中研院週報‧1170期》〈費洛蒙及及應用〉，賀孝雍撰文

高三課本《生物》上冊

費洛蒙香水讓你更有魅力？

坊間有一種費洛蒙香水，宣稱擦了之後會更有異性緣，這是真的嗎？關於人類費洛蒙實驗，最為耳熟能詳的例子是，同一寢室的女生在經過一段時間之後，生理期的日子會變得幾乎相同。此研究是由美國芝加哥大學心理與生物系教授麥克林托克（Martha K. McClintock）在念大學時發現的，當時她兼任女子游泳隊教練，無意間發現女學生的生理期一開始都不一樣，但同住1~2個月後，會出現生理期同步的現象，因此她將此研究發表於1971年《自然》（Nature）期刊。除了受同性影響，也有實驗發現，男性的費洛蒙能調控女性的生理期，使經期不規則的女性恢復正常。

由此可知，人類確實會因為同伴的費洛蒙而影響體內激素的分泌。不過，就費洛蒙香水的功效而言，中央研究院細胞與個體生物學研究所助研究員賀孝雍指出，人類對異性的喜好程度，除了嗅覺，還會被視覺與聽覺影響。換言之，可以增加吸引力的費洛蒙香水是否有效，並不容易檢測，也存在許多疑問，因此不要期望擦了費洛蒙香水，就會變成人見人愛的萬人迷。

【本文轉載自科學人『科學Easy Learn網路版』‧行政院國科會補助案，欲閱讀更豐富內容，請參閱科學人網站http://sa.ylib.com】